
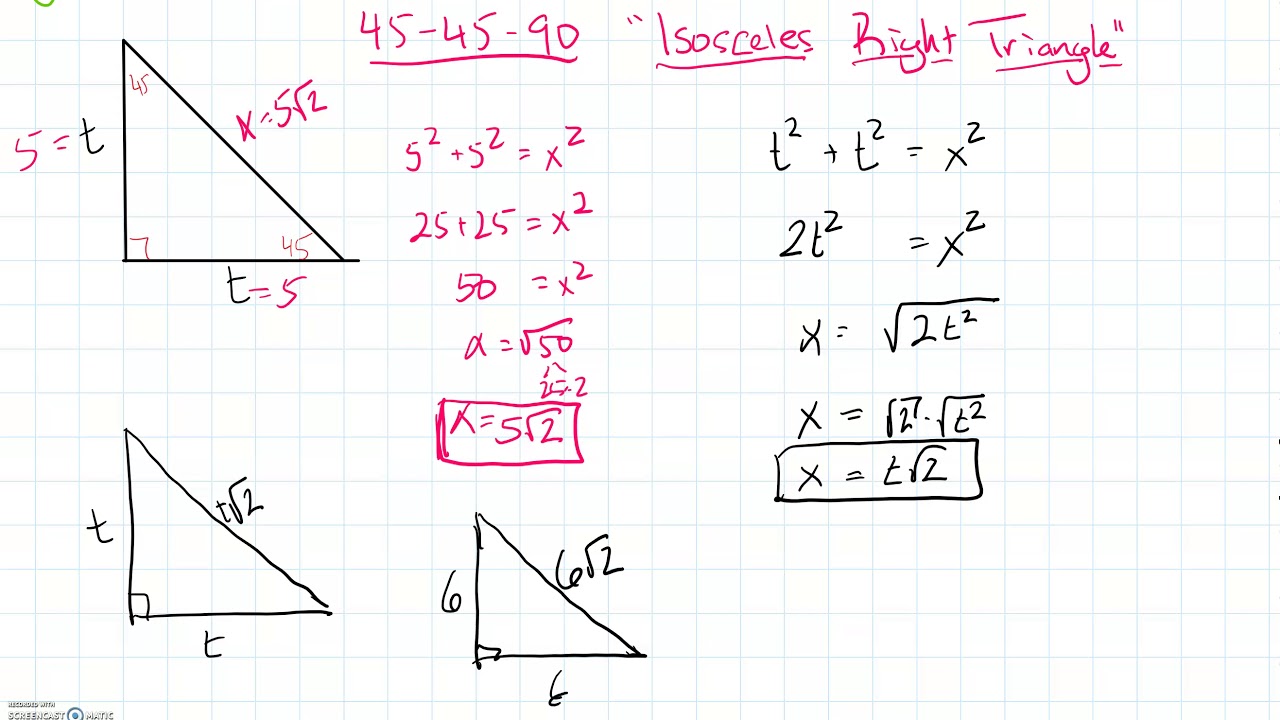
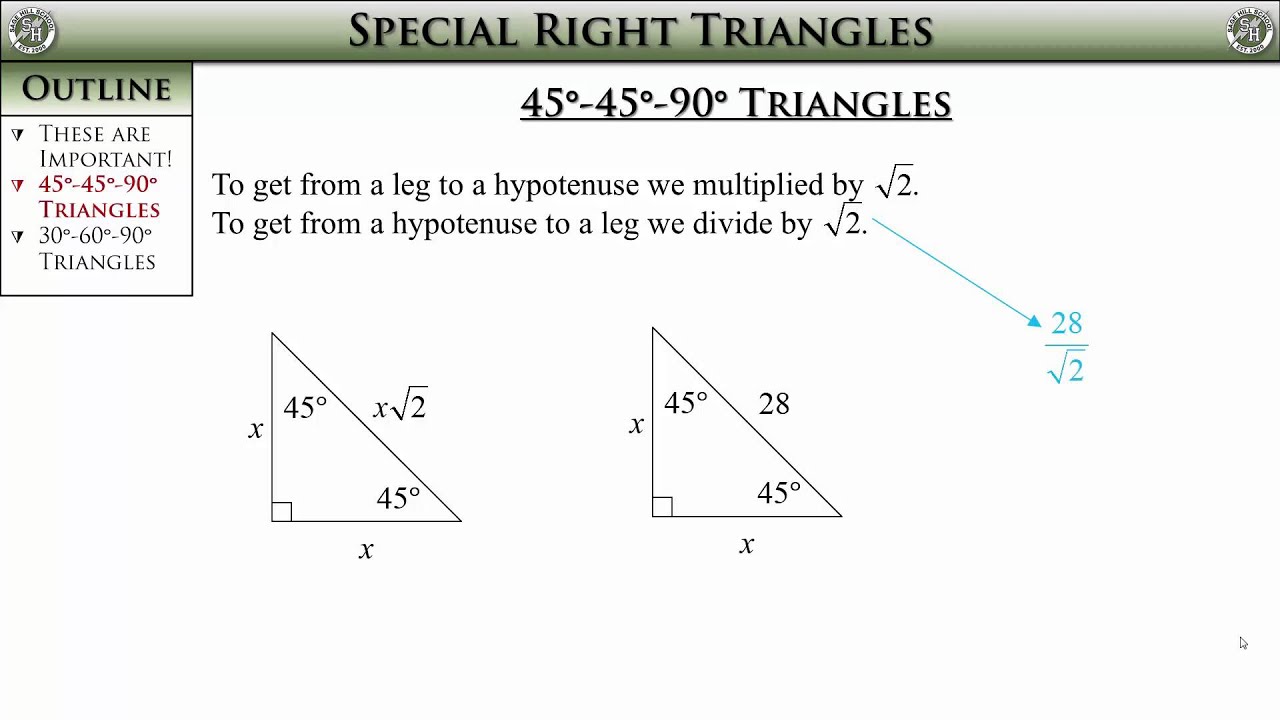
The proportion of the base to height to this triangle’s hypotenuse is 1: 1: √ 2.Now, you can see – Base: Height: Hypotenuse = x: x: x √ 2 = 1: 1: √ 2.Alternatively, a 45 ° 45 ° 90 ° triangle can additionally be an isosceles triangle. An isosceles triangle is a triangle in which two the lengths of its two sides are equal, and likewise, both of its angles are equal.By utilizing the formula of a special right triangle a2 + b2 = c2, we can determine the hypotenuse of a 45 ° 45 ° 90 ° triangle as complies with: Because a 45 ° 45 ° 90 ° triangle is additionally an isosceles triangle let a+ x2= 2×2 Locate the square root of each term in the formula √ x2 + √ x2 = √( 2×2).For that reason, the hypotenuse of a 45 ° 45 ° 90 ° triangle is x √This is a special angle triangle whose angles are 30 ° 60 ° 90 °. The proportion of the lengths of the sides are x: x √ 3: 2x. Learn shortcut ratios for the side lengths of two common right triangles: 45-45-90 and 30-60-90 triangles. The ratios come straight from the Pythagorean theorem.A right triangle formula is provided by a2 + b2 = c2, where either b or a is the triangle’s base and height. By utilizing the Pythagorean Thesis, discovering the absent side of a triangle is relatively easy and straightforward.
“Try to draw a rectangle whose diagonals don’t make 45 degree angles.”One last worry. I should leave the proof up to her, though. So I want to equip her with the means to prove it to herself.Given all this, I think I should probably be more direct in my feedback about the fact of non-bisection. I could ask, “Is it possible to draw a rectangle whose diagonals don’t always make 45 degree angles? The answer matters for what you wrote here.” Or maybe the feedback I supply here should be a counterexample — a very long rectangle whose diagonals clearly don’t make 45 degrees? What’s my goal in this feedback, anyway?I suppose my only goal is to have her know that the diagonals don’t bisect the angles, and to believe this in a way that she’ll remember and be able to reproduce on a new problem. My guess, based on her first triangle, is that she thinks that the diagonal of a rectangle always bisects the right angle.This might make for a nice bit of feedback for her. The first has to do with the Pythagorean Theorem, the other (more interesting) has to do with the angle of inclination.I wonder what she’s looking at that the angle always stays the same.
In conversation, I was able to confirm that my “every rectangle’s diagonals bisect a right angle” theory was right.


 0 kommentar(er)
0 kommentar(er)
